Ellipse is a path traced by a point in such a way that sum of its distances from two fixed points is always constant. The two fix points are known as foci of the ellipse.
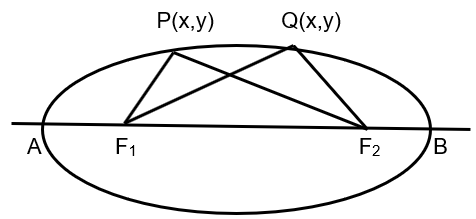
Hence according to the definition sum of the distances of point (x,y) from F1 and F2 is constant. Hence, we can say that PF1 + PF2 = QF1 + QF2 .
Important terms regarding ellipse;
- Major Axis – A line segment which passes through both the foci of ellipse and its end point lie on the ellipse.
- Minor Axis – A line segment running perpendicular to the major axis and passes from the mid-point of the two foci or center of the ellipse.
- Vertices of ellipse – End points of the major and minor axis (which lie on the ellipse) are known as vertices of ellipse.
Remember that length of major axis in an ellipse is 2a units and length of minor axis is 2b units. If the major axis is along / parallel to x-axis then the ellipse is said to be horizontal ellipse; if the major axis is along / parallel to y-axis then the ellipse is said to be vertical ellipse.
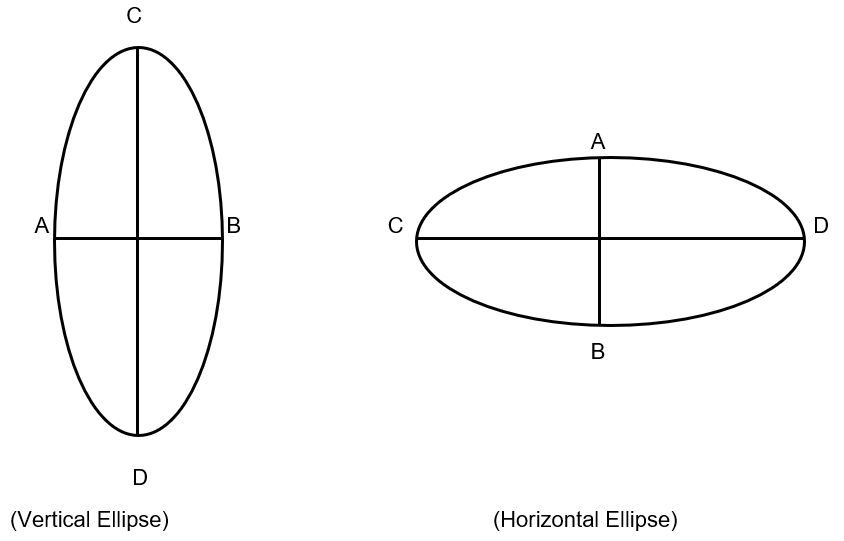
In both the ellipses shown above AB is minor axis and CD is the major axis.
Foci of the ellipse always lie on the major axis.
Eccentricity – In conic section, eccentricity is defined as how deviated the conic section (ellipse, parabola, hyperbola) is from being circle. Eccentricity of circle is defined as 0 or as a reference conic section.
Eccentricity of the ellipse is denoted with the letter ‘e’ which is equal to ‘c/a’, where c2 = a2 – b2. Here a is the length of semi major axis and b is the length of semi minor axis. ‘c’ is also known as the distance between center of the ellipse and one of the foci of the ellipse.
Eccentricity of ellipse is always between 0 and 1.
Latus Rectum – Latus Rectum of an ellipse is a straight line perpendicular to major axis and passes through the foci.
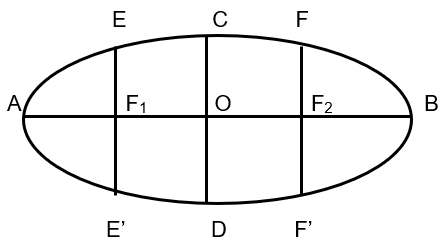
In the figure above EE’ and FF’ are said to be the two latus rectum of the ellipse.
Important result for eccentricity
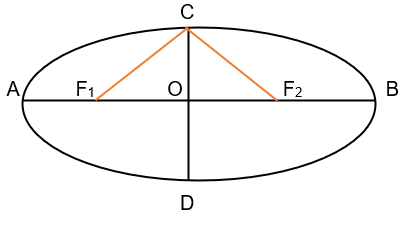
In the above figure;
- AB = 2a units
- CD = 2b units
- F1F2 = 2c units
- Using the above three, we can say that AF1 = BF2 = (a-c) units and using Pythagoras theorem in triangle COF2 we can say that CF2 = √(c2 + b2).
Now, using the definition of ellipse, we can say that CF1 + CF2 = AF1 + AF2
Hence, 2√(c2 + b2) = (a-c) + (a+c);
2√(c2 + b2) = 2a;
√(c2 + b2) = a; ( now squaring both sides)
c2 + b2= a2 or c2 = a2 – b2 (Important result in order to calculate eccentricity)
Standard equation of horizontal ellipse
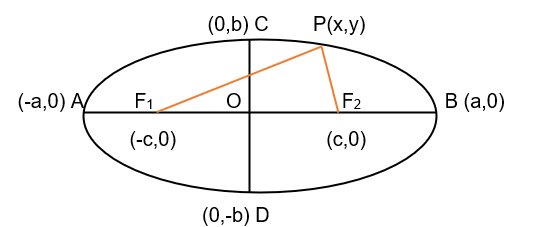
Now in order to calculate the standard equation of ellipse, we’ll be using PF1 + PF2 = AF1 + AF2 (since sum of the distances is constant) or we can also say that PF1 + PF2 = 2a.
√{(x – c)2 + y2} + √{(x + c)2 + y2} = 2a (using distance formula)
√{(x + c)2 + y2} = 2a – √{(x – c)2 + y2}
Squaring both the sides, we’ll get
{(x + c)2 + y2} = 4a2 + {(x – c)2 + y2} – 4a√{(x – c)2 + y2}
On solving this further, we’ll get
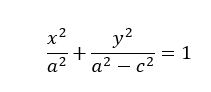
Or, the equation can be written as;
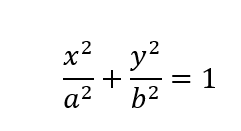
The above equation is known as the general equation of the horizontal ellipse, whose center is at the origin and (a>b).e
If in case the center of the ellipse lies at (h,k), then equation of the ellipse would be;
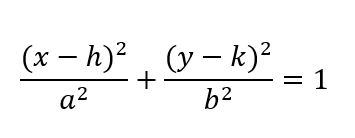
Standard equation of vertical ellipse
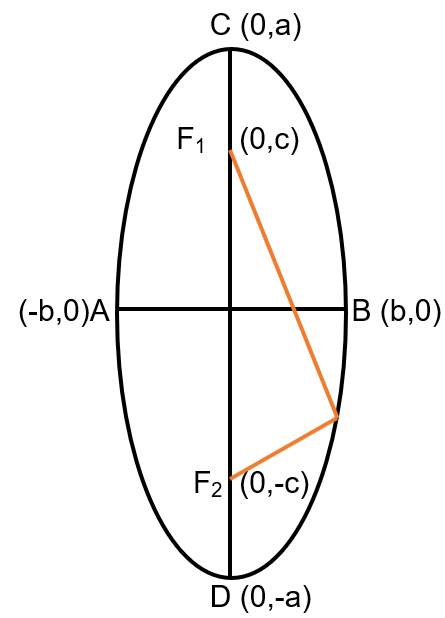
The proof for standard equation of vertical ellipse is exactly the same as that of horizontal ellipse.
There are couple of things which changes when you move to vertical ellipse from horizontal ellipse, such as;
- The major axis is along y-axis.
- Foci now lie on the vertical axis.
The equation of vertical ellipse with center of ellipse lying on origin shall become;
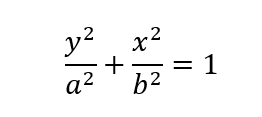
If in case the center of the ellipse lies at (h,k), then equation of the ellipse would be;
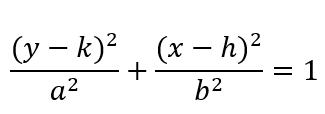
Latus Rectum of ellipse
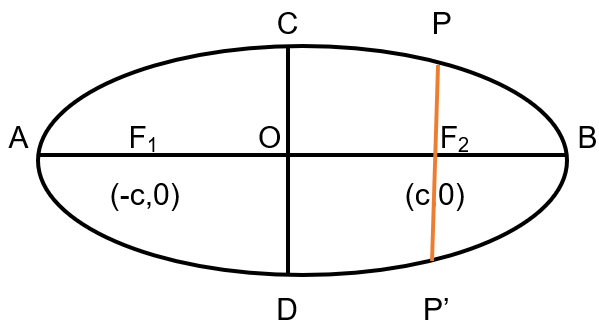
We need to find length of PP’. The two point P and P’ are vertically above and below F2, hence we can say that x-coordinate of P and P’ will be c. In order to calculate y-coordinate of P or P’, we need to replace x by c in the general equation of ellipse and hence we’ll get y-coordinate of P or P’ to be ‘b2/a’ and hence length of PP’ will be 2b2/a.
Hence length of latus rectum of an ellipse is 2b2/a.
